Mulgrido A research project of Stefan Häfner at Institute of Structural Mechanics at Bauhaus-University Weimar, supervised by Prof. Dr.-Ing. habil. Carsten Könke.
1 Introduction
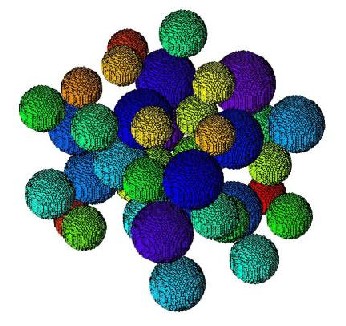
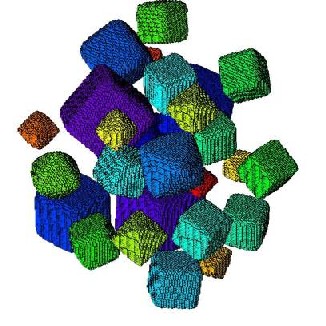
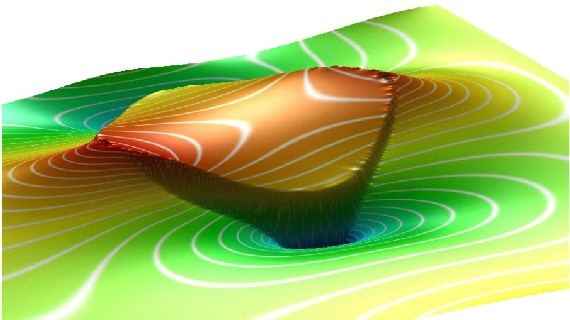
2 Selected Screenshots 3 First Version of Mulgrido 4 Publications 5 Abstract of thesis 6 Download Section > Impressum 1 IntroductionMulgrido is a small finite element program to solve large problems in the analysis
of heterogeneous materials such as concrete. As a main option various controlled
random geometries of concrete can be generated according to provided data of
the concrete mix design. This includes, e.g., sizes, grading, volume and
shapes of aggregates. The mechanical problem on the mesoscale is defined
according to the standard finite element method. Aim of this work is to
analyse strains, stresses, the effective properties and the damage behaviour
of the heterogeneous material. The complexity of the geometry on the
mesoscale potentially leads to very large numerical problems. Therefore an
economical data management and a fast solving strategy was required. The
multigrid method inspired for this new program. First coding started in
summer 2003 and a major rewrite was in spring 2004. Please get some visual
impressions in Section 2 and read more about Mulgrido in Sections 3 to
5.
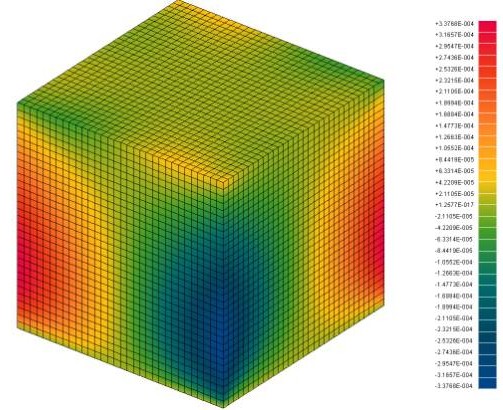
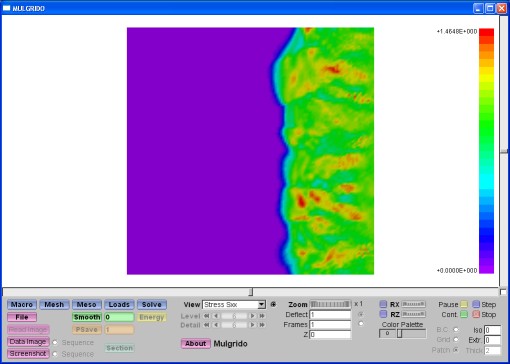
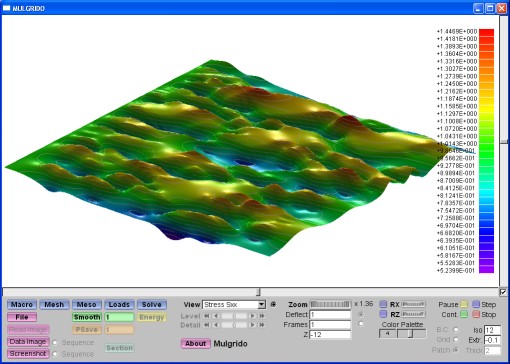
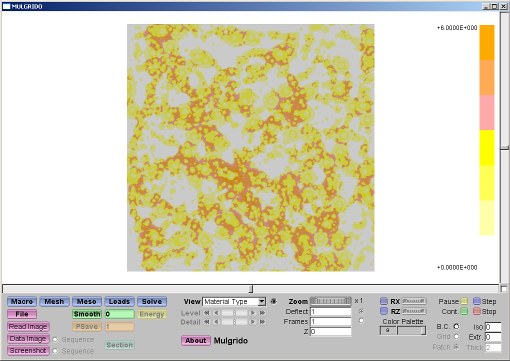
2 Selected Screenshots3 First Version of MulgridoThe first version of Mulgrido was written in C for Linux using the g2-graphics library (2D) and did not include a user interface. The OpenGl rendering machine (3D) and a graphical user interface by the FLTK (Fast Light Toolkit) library replaced this restrictive programming environment of the first version. The current version of Mulgrido compiles on Linux, Macintosh and Windows. It is more efficient and flexible such that the first version sinks into oblivion. Nevertheless, it is worth to include some very first impressions from the program which might still hold some fascination. This example shows the result of a tension test in horizontal direction of a solid with a hard, square inclusion. 4 PublicationsHäfner, Stefan (2007). Grid-based procedures for the mechanical analysis of heterogeneous solids. Ph.D. thesis, Institute of Structural Mechanics, Faculty of Civil-Engineering, Bauhaus-University Weimar. (Please find abstract of thesis also in Section 5.) Häfner, S., S. Eckardt, T. Luther and C. Könke (2006). Mesoscale modeling of concrete: Geometry and numerics. Computers and Structures 84, 450 – 461. Häfner, S., M. Kessel and C. Könke (2006). Multiphase B-spline finite elements of variable order in the mechanical analysis of heterogeneous solids. In K. Gürlebeck and C. Könke (Eds.), Proceedings of IKM 2006, 17th International Conference on the Applications of Computer Science and Mathematics in Architecture and Civil Engineering, 12-14 July 2006, Bauhaus-University Weimar. Häfner, S. and C. Könke (2006). Multigrid preconditioned conjugate gradient method in the mechanical analysis of heterogeneous solids. In K. Gürlebeck and C. Könke (Eds.), Proceedings of IKM 2006, 17th International Conference on the Applications of Computer Science and Mathematics in Architecture and Civil Engineering, 12-14 July 2006, Bauhaus-University Weimar. Häfner, S. and C. Könke (2006). Damage simulation of heterogeneous solids by nonlocal formulations on orthogonal grids. In K. Gürlebeck and C. Könke (Eds.), Proceedings of IKM 2006, 17th International Conference on the Applications of Computer Science and Mathematics in Architecture and Civil Engineering, 12-14 July 2006, Bauhaus-University Weimar. Kessel, Marco (2005). Implementierung rechteckiger Scheibenelemente mit B-Spline Ansätzen n-ter Ordnung. Diploma thesis, Institute of Structural Mechanics, Faculty of Civil-Engineering, Bauhaus-University Weimar. Häfner, S. and C. Könke (2004). A multigrid finite element method for the mesoscale analysis of concrete. In P. Neittaanmäki, T. Rossi, K. Majava and O. Pironneau (Eds.), Proceedings of ECCOMAS 2004, Fourth European Congress on Computational Methods in Applied Sciences and Engineering, 24-28 July 2004, Jyväskylä, Finland. Häfner, S. (2003). Effiziente FEM-Multiskalenkonzepte zur Analyse heterogener Materialien. Forschungskolloquium Baustatik–Baupraxis, 17.–20. September 2003, Universität der Bundeswehr München-Neubiberg. Häfner, S., S. Eckardt and C. Könke (2003). A geometrical inclusion-matrix model for the finite element analysis of concrete at multiple scales. In K. Gürlebeck, L. Hempel and C. Könke (Eds.), Proceedings of IKM 2003, 16th International Conference on the Applications of Computer Science and Mathematics in Architecture and Civil Engineering, 10-12 Juni 2003, Bauhaus-University Weimar. 5 Abstract of thesis The importance of modern simulation methods in the mechanical analysis of
heterogeneous solids is presented in detail. Thereby the problem is noted
that even for small bodies the required high-resolution analysis reaches
the limits of today’s computational power, in terms of memory demand
as well as acceptable computational effort. A further problem is that
frequently the accuracy of geometrical modeling of heterogeneous bodies is
inadequate.
The present work introduces a systematic combination and adaption of grid-based methods for achieving an essentially higher resolution in the numerical analysis of heterogeneous solids. Grid-based methods are as well primely suited for developing efficient and numerically stable algorithms for flexible geometrical modeling. A key aspect is the uniform data management for a grid, which can be utilized to reduce the effort and complexity of almost all concerned methods. A new finite element program, called Mulgrido, was just developed to realize this concept consistently and to test the proposed methods. Several disadvantages which generally result from grid discretizations are selectively corrected by modified methods. The present work is structured into a geometrical model, a mechanical model and a numerical model. The geometrical model includes digital image-based modeling and in particular several methods for the theory-based generation of inclusion-matrix models. Essential contributions refer to variable shape, size distribution, separation checks and placement procedures of inclusions. The mechanical model prepares the fundamentals of continuum mechanics, homogenization and damage modeling for the following numerical methods. The first topic of the numerical model introduces to a special version of B-spline finite elements. These finite elements are entirely variable in the order k of B-splines. For homogeneous bodies this means that the approximation quality can arbitrarily be scaled. In addition, the multiphase finite element concept in combination with transition zones along material interfaces yields a valuable solution for heterogeneous bodies. As the formulation is element-based, the storage of a global stiffness matrix is superseded such that the memory demand can essentially be reduced. This is possible in combination with iterative solver methods which represent the second topic of the numerical model. Here, the focus lies on multigrid methods where the number of required operations to solve a linear equation system only increases linearly with problem size. Moreover, for badly conditioned problems quite an essential improvement is achieved by preconditioning. The third part of the numerical model discusses certain aspects of damage simulation which are closely related to the proposed grid discretization. The strong efficiency of the linear analysis can be maintained for damage simulation. This is achieved by a damage-controlled sequentially linear iteration scheme. Finally a study on the effective material behavior of heterogeneous bodies is presented. Especially the influence of inclusion shapes is examined. By means of altogether more than one hundred thousand random geometrical arrangements, the effective material behavior is statistically analyzed and assessed.
6 Download Section
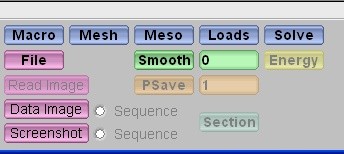
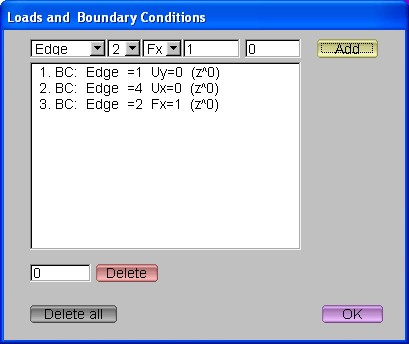
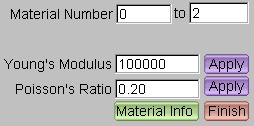
6.1 First ExercisePlease note that Mulgrido is provided at a developer stage and has not been designed to cope with all kinds of possible user interaction at any time. In this context it is refered to Section 6.4. In the following it is described how to run a first example in Mulgrido. The blue buttons are most important (Figure 7). In the beginning these buttons should only be pressed in the following order: Macro, Mesh, Meso, Loads and Solve. In each case a dialog window will open.
Here ends the present description of this example. It is possible to use a few more options in this version of Mulgrido such as e.g. save and load models. 6.2 Second ExerciseThis exercise demonstrates how to load image data into Mulgrido for the definition of an image-based heterogeneous model. The recognized image format is a 24-bit Windows Bitmap (R8 G8 B8) and the expected filename is ”bmpname.bmp”. Such an image can be downloaded here.
For efficient solving, it is useful to choose the multigrid method.
6.3 Download LinksMulgrido is free software, please see Section 6.4. Download of executable program: Mulgrido.exe Version 0.1.0 for Win32 (updated version with loading images option activated) A Linux version is in mulgrido_linux.zip, together with makefile and some additonal information. For sake of stability and intuitive handling, the first published version 0.1.0 of Mulgrido only activates a minor subset of the coded functionality, e.g. B-spline finite elements, three-dimensional modelling and damage analysis are not active in this version. Download of source code: Mulgrido-0-1-0-source.zip The compressed archive includes the full source code. On Windows the Integrated Development Environment (IDE) for the C/C++ programming ”Bloodshed Dev-C++, Version 4.9.9.2” was used, which is free software. The corresponding project file is included in the archive. Also the fluid-file to build the Graphical User Interface (GUI) in FLTK is provided. FLTK is a cross-platform C++ GUI toolkit which supports OpenGL.
6.4 Copyright NoticeMulgrido, a grid-based finite element program. This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/. _____________________________________________________________________ _____________________________________________________________________ Website www.mulgrido.de |